The DFD as a Subsystem-Scope Diagram in the Shlaer-Mellor Method
The DFD is the means by which the derivation of mathematically dependent attributes in the information model is described. Note that this DFD uses different execution semantics from the ADFD and SDFD that are used to describe actions.
A DFD is a set of nodes connected by dataflows. A node represents data associated with an object; and the mathematical function used to derive it, from the dataflows into the node. A dataflow may represent either the flow of data within an object-instance; or the flow of data along a relationship.
The semantics of the DFD are such that all reachable values are recalculated whenever any write accessor is used in an ADFD or SDFD. Write accessors include attribute writes, object creation, object deletion and subtype migration. It is expected that an implementation would optimize the update process to avoid unnecessary recalculations, possibly delaying calculations until an effected attribute is read; and possibly caching the result of these calculations.
Semantics
Nodes
A node represents data associated with an object; and the mathematical function used to derive it from the dataflows into the node. The data may be associated with a attribute. In this case, the information is available to read accessors and persists between DFD recalculations. Nodes associated with attributes are known as "attribute-nodes" and are shown on the Object Information Model. Other nodes, "transient-nodes" represent transient data that exists only as the result of a calculation. At the start of a recalculation, transient data is reset to its null value. A atribute node is part of the system-state; but a transient node is not.
Attributes nodes represent attributes; and so must conform the rules of attribution that govern attributes. Transient nodes do not represent attributes, and are not required to conform to the rules of attribution. Most importantly, a transient node can represent a set of values.
A third type of node is an object. Dataflows from object nodes carry no information: they either exist, or don't exist (but, as a notational convenience, attributes can be attached to the flow). Thus, if a calculation needs to know the number of related instances across a relationship, the object-node allows this to be determined without needing to specify an attribute. If an object node has input flows, then it is a derived object (see below).
Dataflows
A dataflow may represent either the flow of data within an object-instance; or the flow of data along a relationship. A dataflow is represented as an arc on the DFD and flows between 2 nodes. If the data flows along a relationship then the flow inherits the relationship's multiplicity and conditionality. Dataflow within an instance is implicitly 1:1. If necessary (e.g. for asymmetric reflexive relationships), the relationship role is also associated with the dataflow.
Each instance of an object has its own instance of a node. Each node instance drives a value onto an instance of the dataflow. The dataflow delivers the data to the set of instances implied by its associated relationship. If the relationship is `M:', `Mc:' or `1c:' then the destination node sees the dataflow as a bag (or set, if desired) comprising the values from each of the source nodes across the relationship. The destination node does not know the identities of the driving instances. If the relationship is `1:'; or is internal to an instance; then the destination sees a single value that is not part of a set. If the driving node is a transient node, then the values referred to may, themselves, be sets. In this case, the analyst can specify that the dataflow should carry the union of these inner-sets.
If a dataflow is a bag of values, then it may be given sequence semantics. This means that the formalism maintains its order. Although the analyst cannot know what that order is: the analyst can make use of it, for example, to calculate the inner product of 2 input flows from a common source.
Subtype Relationships
Dataflows to or from a subtype not not need to navigate via the supertype. Relationships in subtypes are directly available in all subtypes. However, a subtype's relationships are not available from the supertype.
Recalculation: A DFD update
The DFD update is defined to produce an unambiguous result following a perturbation. An implementation must produce results consitant with this description; but would be expected to use a more efficient algorithm.
A recalculation is triggered following any perturbation of the DFD. At the start of the recalculation, the set of all reachable node-instances (from the perturbation) is dertermined. If the write accessor effects multiple attributes, instances or guards, then the set of reachable instances is the union of the sets that can be reached from each of the sources individually. If the accessor deletes or migrates an object, then the reachable set is the union of the reachablesets before and after the delete or migration.
The set of reachable instances is determined by following the relationships that are associated with unguarded flows in the DFD. An unguarded flow either has no guard; or has at least one of its guards released.
Once the set of reachable nodes is determined, all nodes within this set are set to have no value. If a dataflow carries a set of no values, then it is an empty set. If a calculation is meaningless for an input flow with no value then no calculation is performed (the same should be true for any pre-condition failure). The reason for setting all nodes to no value is to establish a base case for any dataflow loops. It also should help implementations to optimise the update process.
The recalculation consists of a number of update cycles; which continue until a cycle causes no changes within the set of reachable instances. The analyst must ensure that the recalulation will terminate. Any dataflow loops must be defined in a way that ensures convergence of the calculation. If a write accessor explicity sets the value of an attribute node then that value will remain throughout the recalculation.
Each update cycle is divided into 2 phases. In the first phase, the value of each node (in the set of reachable instances) is propogated to the outputs of its outgoing dataflows. In the second phase, each node-instance calculates its value from the value of its input dataflows. This calculation is a "pure" function: it has no side effects and contains no state. If an attribute-node has no input dataflows then its value is not recalculated. Also, any nodes whose values are being set they the write accessor (which caused the recalculation) are not recalculated.
If no values change as a result of the second phase of the update, then the recalculation is complete. Otherwise, the two phases are repeated.
Derived Relationships and Objects
If, as a result of the update, a referential attribute is modified then the set of reachable node-instances is recalculated; updates continue using an update set comprising the union of the old and new sets of reachable nodes. Any additional transient nodes in the set are reset to their null value.
If a relationship is formalised in the identifiyer of another object, then the derived relatinship will, naturally, cause the object to be derived. When this happens, we know that there will be exactly one instance of the related object for each instance of the formalising object. However, this relationship may not be 1:1. Only the right hand multiplicity is definitely `1'. A derived object is modelled as an "object-node" with input flows.
If the relationship is 1:1 then the derivation is trivial. Each instance that is represented on the input flow will imply a derived object. The value on the flow is irrelevant. If the relationship is 1c:1 then the a predicate in the object-node will use the value on the flow to define whether the derived object should exist.
When the relationship is M:1 (or Mc:1) then there will exist 1 (or more) attributes in the identifier that are not part of the formalisation of the relationship. However, we know that the identifier of the derived object is mathematically dependent on the related object; so the set of values for the non-formalising attribute is is derived (as a set). In this case, no predicate is needed - an empty set indicates that no objects are derived. If there are multiple non-formalising attributes then the analyst can choose to use either a set of tuples; or a tuple of sets. In the latter case, all possible combinations of objects are created.
The most important use of the derived object is as an associative object. In this case, the input flows to the derived object will come from 2 sources. The ordering of the two input flows will probably be independent; so all combinations will be available as potential objects. As with the previous cases, a 1:(X:X) associative object will be defined with a predicate; and M:(X:X) assoc will be modelled with a set of values of the non-formalising identifier attributes.
Once a derived object exists, its descriptive attributes can be derived in the same way as any other object. However, we should restrict derived objects to being passive.
Time Rules
The analyst may safely assume that a recalculation that is triggered by a write accessor will have completed by the time a read accessor is used to read any value that would be modified as a result of that write access.
The anlayst may also assume that the result of the recalcuation is not effected by the intermediate update cycles of any other recalculation.
These two analysis assumptions place requirements on the implementation.
Guards
A dataflow may be guarded. The output of a guarded flow will not be modified during an update cycle unless that guard is released. A guard is defined by a "change-concept" for modifying an attribute. A guard is released by a write-accessor for its attribute which is explicity qualified with its change-concept.
More than one guard may be associated with a dataflow. If any of its guards is released, then the dataflow behaves like an unguarded flow for the duration of the recalculation. At the end of the translation, all guards are released. Recalulation is then continued with all guards released (this should not cause any further changes to the value of nodes). This rule ensures that guards cannot be used to add additional information storage that is not visible on the OIM. Thus the DFD is a stateless, static, representation of mathematical dependency in the OIM.
Guards are associated with specific instances of dataflows. A write accessor defines a set of instances of an object: guards are only released for those instances of dataflows that are reachable, by following the relationships that are shown the DFD, from the instances identified by the write accessor.
Notation
The DFD is drawn with rectangles for nodes, and lines for dataflows. The rectangle of a transient node has a dotted outline. A dataflow has a single-headed arrow at one end to show the direction of dataflow.
The contents of the node is the name of the object and the name of the attribute or transient. Where the attribute name is unambiguous, the object name may be omitted. The formula or algorithm associated with the node is shown in a "note" box (UML notation).
Dataflows have many more adornments. Each end of the dataflow is adorned with the multiplicity of its corresponding relationship (This can be omitted if its value is `1'). The name of the relationship is written beside the dataflow (where necessary, this includes the relationship role); dataflows within an instance are adorned with the word "this". Guards are shown in Square brackets. These brackets contain 2 text fields, separated by a comma: the name of an attribute and the change-concept for its modification e.g. "[volume, change pressure]"; to avoid ambiguity, the attribute name may be qualified with its object name. Finally, the stereotypes "<<set>>" and "<<bag>>" may be used to indicate that the dataflow is either a set, or a bag, respectively. If ommitted, bag semantics are assumed. The dataflow from a transient node may also specify "<<union>>" to combine a set-of-sets into the union of the inner sets.
When a dataflow travels in both directions along a relationship, a double-ended arrow can be used. In this case,information that is relevant to only one direction of flow (for example, guards ans stereotyes) are placed at the same end as the arrow-head for that direction.
Examples
Balance of an account

This is very simple. The balance of account is the sum of all its transactions. This assumes that debits are negative amounts. Note the use of the <<bag>> stereotype. It's not required, but is a useful reminder. If information is omitted, then it is sometimes difficult to know whether the intent was to use the default, or whether we just plain forgot.
Mass, density, volume triangle
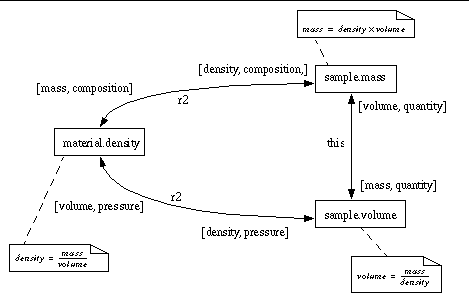
This is a bit more complex. Every attribute in the group is dependent on both the other two. Here, each of the 6 flows is quarded by a qualified write accessor. For eample, the guard in the upper right of the diagram says that if the write accessor for "volume" is invoked, under the concept of "quantity" then the change to the volume can flow down the path from volume to mass. Thus, if the set the volume to change the quantity then the mass is changed but the density isn't (because no other guards are activated.
If we invoke the write accessor for "volume" under the concept of "pressure" then the bottom left guard is activated; so the density is changed but the mass isn't.
Manipulation of a rectangle
This example demonstrates the problems associated with having too much information - the additional complexity is a symptom of an inappropriate level of abstraction for the mathematical dependency.
Consider a simple DFD for a rectangle. The length and width attributes determine the area and aspect ratio of the rectangle:
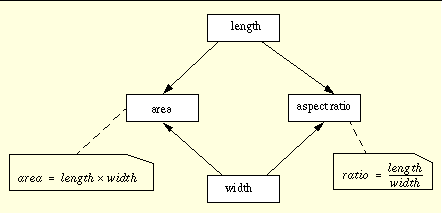
This is fine, but what if I want to change it to have 2 change-concepts: "size" and "shape" (actually, "constant shape" and "constant area"). The dataflows become bidirectional. Its easy to see how to place the guards but we need a few extra derivations:
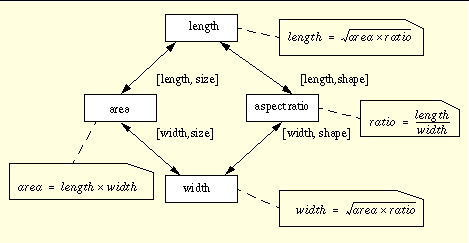
Unfortunately, this does not meet the requirements of the DFD becasue a recalculation won't converge (or, if it does, then it will be slow). The problem is that we don't have the right dataflows for the concepts being expressed. We actually want to define:
But if we use these derivations, we then need need 2 derivations for the area and ratio nodes.
I haven't found a good solution to this problem yet. The seem to be 2 solutions:
- provide multiple derivations, keyed from the write accessor (i.e. same as guards). The problem is that they must be equivalent.
- Provide a single source for the derivations and require the formalism/translator to do the rearrangement. This seems nicer for the analyst; but is probably not feasible for general purpose use.
A third possibility is to ignore the problem, and say that if you can't force convergence, then you can't represent the concept.